链接
\(\text{2019南京网络赛-B.super_log}\)
题意
有一个分段函数如下: 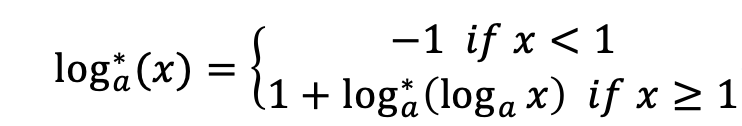 现在需要你找到最小的正整数\(x\),使得\(log_{a}^* (x) \ge b\),由于结果可能会非常大,所以需要你输出\(x\)对\(m\)取余后的结果。
现在需要你找到最小的正整数\(x\),使得\(log_{a}^* (x) \ge b\),由于结果可能会非常大,所以需要你输出\(x\)对\(m\)取余后的结果。
输入格式:共\(t\)组测试样例,每组样例有一行,一行三个数\(a,b,m\).
\(\text{2019南京网络赛-B.super_log}\)
有一个分段函数如下: 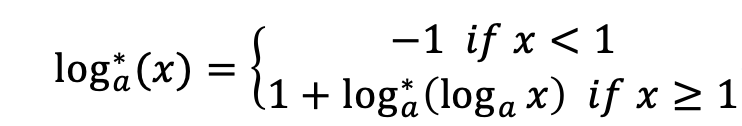 现在需要你找到最小的正整数\(x\),使得\(log_{a}^* (x) \ge b\),由于结果可能会非常大,所以需要你输出\(x\)对\(m\)取余后的结果。
现在需要你找到最小的正整数\(x\),使得\(log_{a}^* (x) \ge b\),由于结果可能会非常大,所以需要你输出\(x\)对\(m\)取余后的结果。
输入格式:共\(t\)组测试样例,每组样例有一行,一行三个数\(a,b,m\).
\(\text{2019南京网络赛-A.The beautiful values of the palace}\)
有一个\(n\times n\)的螺旋数字矩阵,\(n\)一定是奇数,若边长为5则如下:

这个矩阵内有\(m\)个点是有效的(即有一个值为对应螺旋矩阵该位置的值),其他位置都为0。现在有\(p\)次查询\((x1,y1,x2,y2)\),询问\((x1,y1,)、(x2,y2)\)所围成的矩阵之间的所有数的数位和的和是多少。
输入格式:共\(t\)组测试样例,每组样例,第一行三个数\(n,m,p\),接下来\(m\)行,每行一组坐标\((x,y)\),告诉\(m\)个有效点,之后\(p\)行,每行一次查询\((x1,y1,x2,y2)\)。
数据范围:\((t\leq 5,n\leq 10^6),(m,p\leq 10^5)\).
输出格式:每行输出一个查询结果。
\(\text{2019宁夏网络赛-F.Moving On}\)
有\(n\)个城市,城市\(i\)有一个犯罪值\(r_i\),城市u和v之间的距离是\(d[i][j]\)(无向图),现在有\(q\)次查询,每次查询询问从城市\(u\)到\(v\),在中途经过的任意城市的犯罪值不超过\(w\)的情况下(中途城市不包括\(i\)和\(j\))的最短路径是多少。
\(\text{2019宁夏网络赛-A.Maximum Element In A Stack}\)
给你一个空的\(\text{stack}\),你有两种操作,入栈一个数以及将栈顶数出栈,每次入栈操作后或者出栈操作后,你需要输出当前栈中的最大值,如果栈为空而当前操作为出栈,那么应该输出0。
输入规格即数据范围:第一行一个\(\text{T(T<50)}\),下面每行一组测试样例,包含七个整数\(n(1\leq n \leq 5\times\ 10^{6}),p,q,m(1\leq p,q,m\leq 10^{9}),SA,SB,SC(10^{4}\leq SA,SB,SC\leq 10^{6})\),其中\(n\)是操作的数量,其中关于入栈出栈操作部分代码已给出,如下:
网络爬虫可以按照指定的规则(网络爬虫的算法)自动浏览或抓取网络中的信息,通过Python可以很轻松地编写爬虫程序或者是脚本。
如百度的爬虫,它的名字叫做百度蜘蛛,它是百度搜索引擎的一个自动程序。它每天都会在海量的互联网信息中进行爬取,收集并整理互联网上的网页、图片视频等信息。然后当用户在搜索引擎中输入对应的关键字时,百度将从收集的网络信息中找出相关的内容,按照一定的顺序将信息呈现给用户。
\(\text{Luogu-P1352 没有上司的舞会}\)
\(\text{Ural}\)大学有\(N\)名职员,编号\(1\dots N\),它们的关系是一棵以校长为根的树,父节点即是子结点的直接上司。每个职员有一个快乐指数\(H_i\)。现在这里有一场宴会,但是没有职员愿意和直接上司一起参会,在此条件下,主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,输出这个最大值。
数据范围:\(1\le N \le 6000,-128\le H_i\le 127\).
这是一个类似于祖玛的游戏,你有一个长度为\(\text{N}\)的序列\(c\),序列中一个联通块可以消去(即删除,类似消一消,只能一个联通块一个联通块的消去),一个联通块即是一个连续的子序列,且该子序列是回文的,一个联通块被消去就不存在了,问最少需要消几次。
数据范围:\(1\le N \le 500,1\le c_i\le N\).
给定一个字符串\(\text S\) ,最少需要几次增删改操作可以把\(\text S\)变成一个回文字符串?一次操作可以在任意位置插入一个字符,或者删除任意一个字符,或者把任意一个字符修改成任意其他字符。输出最少的操作次数。
数据范围:字符串\(\text S\)。\(\text S\)的长度不超过\(100\), 只包含\(\text{A-Z}\)。
\(\text{Bessie}\)在一个直赛道上跑步,他需要跑\(\text{N}\)分钟,其中第\(i\)分钟他能跑\(d_i\)米,同时他还有一个最大疲劳值\(M\),开始的时候它的疲劳值为\(0\),跑步的时候每一分钟他都可以选择跑与不跑,如果跑的话,他的疲劳值就会增加\(1\),如果选择休息,他的疲劳值就会下降,但是他只能等疲劳值下降到\(0\)才能再次跑,现在你需要求出\(\text N\)分钟之后,他的疲劳值为\(0\)时他能跑的最大距离是多少。
数据范围:\(1\leq \text{M} \leq 500\),\(1\le d_i\le 1000\).