[HDU-4292] Food

发表于 | 分类于 ， ，
本文字数： 16k

链接

\(\text{HDU - 4292 Food}\)

题意

  这里有\(N\)个人、然后提供\(F\)种食物、\(D\)种饮料，并且对于\(F\)种食物、\(D\)种饮料，仅仅分别提供有限数量\(a_i,b_i\)，现在对于\(n\)个人，给出每一个人喜欢食物和饮料的编号，现问最多可以可以让多少人感到满足；如果一个人可以获得任意一份他喜欢的食物和任以一份他喜欢的饮料，那么他会感到满足；

  数据范围：多组测试样例，\(1\leq N,M,D\leq 200\).

分析

  这一题需要使用最大流，所以关键部分是怎么建图；

  对于每个人，我们都已知他喜欢得到的食物和饮料的编号，我们需要给人与饮料、人与食物之间建立边，边权为1（每个人仅需获得一份食物和饮料即可满足）；并且我们想要满足更多的人，而如果一个人能够满足，那么我们可以看成是，有一个流量大小为1的流，按顺序流经食物、人、饮料（或者饮料、人、食物也可以），那么显然的我们需要定义一个起点，这个起点连接所有食物，这样一条边的容量即是该种食物的数量，同样我们需要连接所有饮料到一个汇点，这里就建立起了一个网络流，我们需要求出起点到汇点的最大流量；

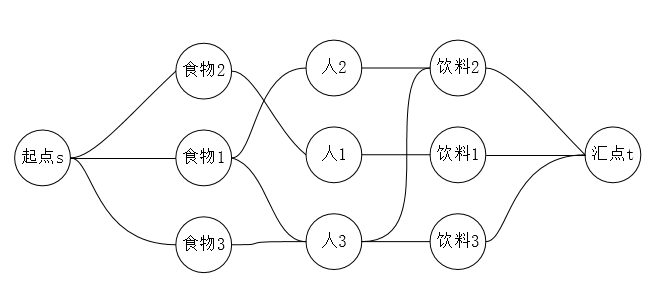
  然而这里还有一些问题，如下图：

  这个图可能存在这样的情况，某一个人可能选择多于1份的食物或者饮料，所以对于任意一个人，我们需要将他看作两个节点，这两个节点相连接，流量为1，这样就能保证整个人最多只能选择一份食物和一份饮料。

  这题和Poj3281几乎是一样的；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <queue>
#include <string>
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
#include <cmath>
#include  <vector>
#define clr(a, b) memset(a, b, sizeof(a))
#define inf 0x3f3f3f3f

using namespace std;

typedef long long ll;

struct node{
    int to,val,pre,next; 
}e[3000005];

int cnt, head[200005];

inline void add(int x,int y,int w) 
{
    e[cnt].pre=x;
    e[cnt].to=y;
    e[cnt].val=w;
    e[cnt].next=head[x];
    head[x]=cnt++;
    e[cnt].pre=y;
    e[cnt].to=x;
    e[cnt].val=0;
    e[cnt].next=head[y];
    head[y]=cnt++;
}

int t, n, f, d, v[200005], dis[200005];

int bfs() {
    for (int i = 0; i <= t; i++)
        dis[i]=0;
    queue<int> q;
    q.push(0);
    dis[0] = 1;
    while (q.size()) {
        int x = q.front();
        q.pop();
        for (int i = head[x]; i != -1; i=e[i].next) {
            if (e[i].val && !dis[e[i].to]) {
                q.push(e[i].to);
                dis[e[i].to] = dis[x] + 1;
                //cout << dis[e[i].to] << " " << e[i].to << endl;
                if (e[i].to == t) return 1;
            }
        }
    }
    return 0;
}

int dinic(int x, int flow) {
    if (x == t) return flow;
    int res = flow, k;
    for (int i = head[x]; i != -1 && res; i=e[i].next) {
        int val = e[i].val, v = e[i].to;
        if (val && dis[v] == dis[x] + 1) {
            k = dinic(v, min(res, val));
            if (!k) dis[v] = 0;
            e[i].val -= k;
            e[i ^ 1].val += k;
            res -= k;
        }
    }
    return flow - res;
}

int main() {
    //freopen("test.in", "r", stdin);
    //freopen("test.out", "w", stdout);
    while (cin >> n >> f >> d ) {
        cnt = 0;
        t = 2 * n + f + d + 1;
        for (int i = 0; i <= t; i++)
            head[i]=-1;
        int x;
        for (int i = 1; i <= f; i++) {
            scanf("%d", &x);
            add(0, 2 * n + i, x);
        }
        for (int i = 1; i <= d; i++) {
            scanf("%d", &x);
            add(f + 2 * n + i, t, x);
        }
        for (int i = 1; i <= n; i++) 
            add(i, n + i, 1);
        string s;
        for (int i = 1; i <= n; i++) {
            cin >> s;
            for (int j = 1; j <= f; j++) {
                if (s[j - 1] == 'Y') add(2 * n + j, i, 1);
            }
        }
        for (int i = 1; i <= n; i++) {
            cin >> s;
            for (int j = 1; j <= d; j++) {
                if (s[j - 1] == 'Y') 
                    add(n + i, n + n + f + j, 1);
            }
        }
        int flow = 0, maxflow = 0;
        while (bfs()) {
            while (flow = dinic(0, inf)) maxflow += flow;
        }
        cout << maxflow << endl;
    }
}