[POJ - 1185] 炮兵阵地

发表于 | 更新于 | 分类于 ， ，
本文字数： 14k

链接

\(\text{POJ - 1185 炮兵阵地}\)

题意

  给你一个\(N\times M\)的网格地图，这个地图上的每一格上如果是H则代表山地，若是P则代表平原，在平原上可以布置一只炮兵部队（山地上不能部署部队），一只炮兵的攻击范围如下。

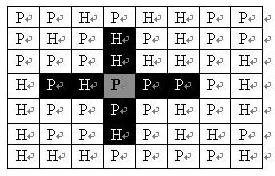
  现在需要你在这张\(N\times M\)的地图上部署部队，在避免误伤的前提下（即任意一支部队都不在其他部队的攻击范围之内），问你最多能布置多少只部队。

  输入格式：第一行输入\(N,M\)，之后输入一个\(N\times M\)的使用H和P表示的地图。

  输出格式：输出最多可以布置的部队的数量。

  数据范围：\(N\leq 100,M\leq 10\)

分析

  如果攻击范围为沿纵横各延伸1格，那么我们将第\(i\)行作为阶段，每一行部队的布置情况作为状态，那么枚举两层（第\(i\)和第\(i-1\)行）的可行状态，进行转移即可，然而这里的攻击范围波及到了第\(i-2\)行，所以我们还要考虑第\(i-2\)行的状态。

  将放置部队的位置置为1，首先预处理一下所有的可行的状态（即相邻两个\(1\)之间的距离不小于3），用\(f[i][j][k]\)表示第\(i\)行的状态为\(j\)第\(i-1\)行的状态为\(k\)时，前\(i\)行最多能放置多少个部队，考虑\(f[i-1][k][l]\)向\(f[i][j][k]\)转移，那么有：

\[f[i][j][k]=\max{f[i-1][k][l]}+sum(i)\]

  在满足状态\(j\)不与状态\(k\)和\(l\)冲突的情况下，\(sum(i)\)即是这种情况下的第\(i\)行状态\(j\)的\(1\)的个数，还需要预处理一下地图的状态，保证每行地图的状态与每一行布置部队的状态不冲突（即只能在P位置布置部队），还要预处理一下每一行\(((1<<M)-1)\)个状态中的可行的状态（即相邻两个\(1\)之间的距离不小于\(3\)的状态），\(M\)为\(10\)的时候最多有\(60\)个，存储信息的\(f\)数组的第二维第三维最大开\(61\)即可（用来保存可行状态），之后逐行进行状态转移即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#include <ostream>
#include <queue>
#include <set>
#include <stack>
#include <string>
//#include <unordered_map>
#include <vector>

using namespace std;

typedef long long ll;

const int M = 11;
const int N = 102;

int n, m, sta[65], sum[65], cnt, dp[1 << M][65][65], pk[105];
char s[M];

void init() {
    //相邻两个炮兵距离不超过3的这种状态的处理，最多只有60个
    for (int i = 0; i < 1 << m; i++){
        if (!(i & (i << 1)) && !(i & (i << 2))) {
            sta[++cnt] = i;
            int j = i, cot = 0;
            while (j) {
                j -= j & -j;
                cot++;
            }
            sum[cnt] = cot;
        }
    }
}

int main(){
	//freopen("test.in", "r", stdin);
    //freopen("test.out", "w", stdout);
    cin >> n >> m;
    init();
    for (int i = 1; i <= n; i++) {
        cin >> s;
        for (int j = 0; j < m; j++) {
            if (s[j] == 'H')
                pk[i] += (1 << j);
        }
    }
    for (int i = 1; i <= cnt; i++) {
        if (!(sta[i] & pk[1])) {
            for (int j = 1; j <= cnt; j++)
                dp[1][i][j] = sum[i];
        }
    }

    for (int i = 2; i <= n; i++) {
        for (int j = 1; j <= cnt; j++) {
            if (pk[i] & sta[j]) continue;
            for (int k = 1; k <= cnt; k++) {
                if (sta[k] & sta[j]) continue;
                if (sta[k] & pk[i - 1]) continue;
                for (int p = 1; p <= cnt; p++) {
                    if (sta[p] & sta[k]) continue;
                    if (sta[p] & sta[j]) continue;
                    if (pk[i - 2] & sta[p]) continue;
                    dp[i][j][k] = max(dp[i][j][k], dp[i - 1][k][p] + sum[j]);
                }
            }
        }
    }
    int ans = 0;
    for (int i = 1; i <= cnt; i++)
        for (int j = 1; j <= cnt; j++)
            ans = max(ans, dp[n][i][j]);
    cout << ans << endl;
}