[POJ - 2411] Mondriaan's Dream

发表于 | 更新于 | 分类于 ， ，
本文字数： 13k

链接

\(\text{POJ - 2411 Mondriaan's Dream}\)

题意

  求把\(N\ast M\)的棋盘分割成若干个\(1\ast 2\)的长方形，有多少种方案。如\(N=2，M=4\)，有\(5\)种方案，\(N=2，M=3\)有\(3\)种方案：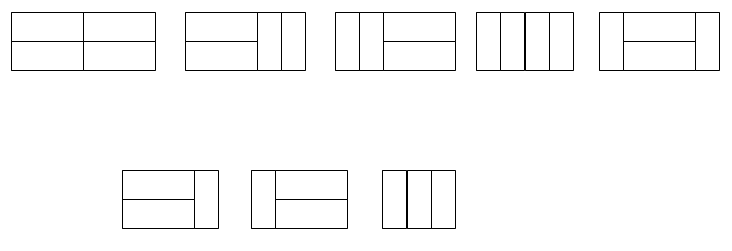

  输入格式：输入包含多组样例，每行一个样例，每个样例一行两个数\(N,M\).

  数据范围：\(1\leq N,M\leq 11\).

  输出格式：每个样例输出一行代表方案数。

分析

  总共\(N\)行\(M\)列，考虑将每一列的长方形的摆放当作状态，第\(i\)行即是第\(i\)阶段；

  将长方形的状态定义为如下：

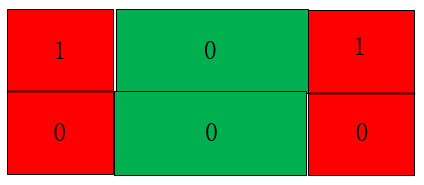
  使用一个\(M\)位二进制数，若第\(j(0\leq j<M)\)位为\(1\)，则表示这个位置是一个竖着的长方形的上半部，为0则是其他情况，\(f[i][j]\)表示第\(i\)行的状态为\(j\)时，前\(i\)行分割方案的总数，当第\(i\)的状态\(j\)能向第\(i+1\)行状态\(k\)转移时，必有\((j\&k)==0\)，且\(j|k\)的结果中每一段连续的\(0\)都必须有偶数个

   我们可以从\([0,(1<<M)-1]\)中预处理出并记录，二进制表示下连续的\(0\)有偶数个的所有状态，记录在\(S\)集合中。

\[f[i][j]=\sum_{j\&k=0\space and\space j|k\in S} f[i-1][k]\]

  初始值\(f[0][0]=1\)，其余为0，目标为\(f[N][0]\)，复杂度为\(O(4^MN)\).

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#include <ostream>
#include <queue>
#include <set>
#include <stack>
#include <string>

#include <vector>

#define INF 0x7f7f7f7f
#define MAXN 1000005
#define N 200005
#define P 2
//#define MOD 99991
#define MOD(a, b) a >= b ? a % b + b : a

typedef long long ll;

namespace fastIO {
    //#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1<<22, stdin),
    // p1 == p2) ? EOF : *p1++) char buf[(1 << 22)], *p1 = buf, *p2 = buf;
    inline int read() {
        char c = getchar();
        int x = 0, f = 1;
        while (c < '0' || c > '9') {
            if (c == '-')
                f = -1;
            c = getchar();
        }
        while (c >= '0' && c <= '9')
            x = x * 10 + c - '0', c = getchar();
        return x * f;
    }
}  // namespace fastIO

using namespace fastIO;
using namespace std;

int h, w;
ll f[12][1 << 12], sta[1 << 12];
int main() {
    //freopen("test.in", "r", stdin);
    //freopen("test.out", "w", stdout);
    while (scanf("%d%d", &h, &w) != EOF) {
        if (!h || !w) break;
        memset(f, 0, sizeof(f));
        memset(sta, 0, sizeof(sta));
        //预处理二进制表示下每一段连续的0都有偶数个的状态
        for (int i = 0; i < 1 << w; i++) {
            int odd = 0, cnt = 0;
            for (int j = 0; j < w; j++)
                if (i >> j & 1) odd |= cnt, cnt = 0;
                else cnt ^= 1;
            sta[i] = odd | cnt ? 0 : 1;
        }
        f[0][0] = 1;
        for (int i = 1; i <= h; i++)
            for (int j = 0; j < 1 << w; j++)
                for (int k = 0; k < 1 << w; k++)
                    if (sta[j | k] && (j & k) == 0)
                        f[i][k] += f[i - 1][j];
        cout << f[h][0] << endl;
    }
}