[Luogu-P1122] 最大子树和

发表于 | 更新于 | 分类于 ， ，
本文字数： 12k

链接

\(\text{Luogu - P1122 最大子树和}\)

题意

  这里有一株花卉，上面共\(n\)朵花，共\(n-1\)条枝干将花儿连在一起，每朵花都有一个美丽指数，数越大说明花越漂亮，也有美丽指数为负的，现在你需要取修剪这株花卉，修剪意味：去掉其中一条枝条，这样就得到了两株，然后丢掉其中一株，继续修剪；最后还剩下一株花，现在你需要修剪最初的花卉，使得最终剩下的一株花卉上所有花朵的美丽指数之和最大。

  输入格式：第一行一个整数\(n\)，\(n\)表示初始花卉上花朵的数量，第二行\(n\)个整数，其中第\(i\)个表示第\(i\)朵花的美丽指数，接下来\(n-1\)行，每行两个整数\(a、b\)，表示存在一条连接第\(a\)朵花和第\(b\)朵花的枝条。

  数据范围：\(1\leq n\leq 16000\).

  输出格式：输出一行，修剪后得到的美丽指数之和的最大值，保证绝对值不超过2147483647.

分析

  开始，我们需要考虑作为树形\(dp\)的树根是谁。

  后来发现不需要考虑这个问题

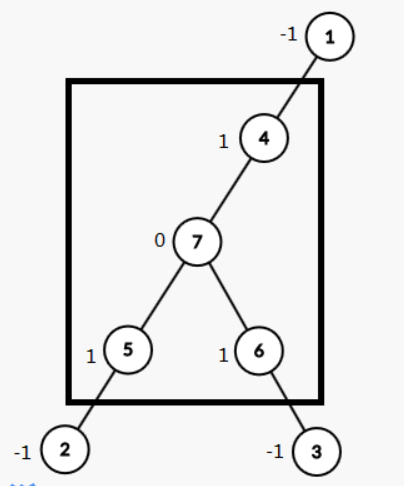
  对于如图的一棵树，我们最后得到的结果是方框中的部分，左下角的2和右下角的3以及右上角的3都被切掉了。那么我们可以考虑在\(dp\)的过程中进行切的操作。

  使用\(f[i]\)，表示在以\(i\)为根的子树中进行修剪的操作能获得花卉所有花朵美丽指数之和的最大值，其中保留根\(i\)，那么显然，无论以谁为根进行修剪，在修剪过程中，总有以某个结点为子树根能获得最大的美丽指数之和，当我们搜索到一个节点\(x\)，我们遍历它的子树\(y_i\)，我们已经获得了他的子树的所有结果，那么我们显然可以考虑把\(y_i\)的子树部分的答案，切掉或者不切掉，如果它的子树的答案是负的，那么我们显然是不能选它的，只有为正时才选它。所以有： \[f[u]+=\max(0,f[v])\space v\in Son(u)\]

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <ostream>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <unordered_map>
#include <vector>

#define INF 0x7f7f7f7f
#define MAXN 16005
#define N 200005
#define P 2
//#define MOD 99991
#define MOD(a, b) a >= b ? a % b + b : a

typedef long long ll;

namespace fastIO {
    //#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1<<22, stdin),
    // p1 == p2) ? EOF : *p1++) char buf[(1 << 22)], *p1 = buf, *p2 = buf;
    inline int read() {
        char c = getchar();
        int x = 0, f = 1;
        while (c < '0' || c > '9') {
            if (c == '-')
                f = -1;
            c = getchar();
        }
        while (c >= '0' && c <= '9')
            x = x * 10 + c - '0', c = getchar();
        return x * f;
    }
}  // namespace fastIO

using namespace fastIO;
using namespace std;

int n, a, b, va[MAXN], sz[MAXN];
ll res, f[MAXN];
vector<int> vec[MAXN];

void dfs(int u, int fa) {
    f[u] = va[u];
    for (int i = 0; i < vec[u].size(); i++) {
        int v = vec[u][i];
        if (v == fa) continue;
        dfs(v, u);
        f[u] += max(1ll * 0, f[v]);
    }
    res = max(res, f[u]);
}

int main() {
    //freopen("test.in", "r", stdin);
    //freopen("test.out", "w", stdout);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &va[i]);
    }
   for (int i = 1; i <= n - 1; i++) {
        scanf("%d%d", &a, &b);
        vec[a].push_back(b);
        vec[b].push_back(a);
    }
    dfs(1, 0);
    cout << res << endl;
}