[2019南京网络赛-B] super_log

发表于 | 更新于 | 分类于 ， ，
本文字数： 14k

链接

\(\text{2019南京网络赛-B.super_log}\)

题意

  有一个分段函数如下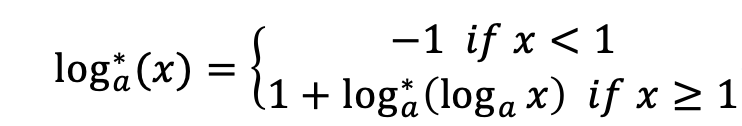：   现在需要你找到最小的正整数\(x\)，使得\(log_{a}^* (x) \ge b\)，由于结果可能会非常大，所以需要你输出\(x\)对\(m\)取余后的结果。

  输入格式：共\(t\)组测试样例，每组样例有一行，一行三个数\(a,b,m\).

  数据范围：\(1\leq a\leq 1000000,0\leq b\leq 1000000\),\(1\leq m\leq 1000000\).

  输出格式：每行对应一个样例结果。

分析

  实际上这里是要计算\(a^{a^{a^{\dots}}}\%m\)这里共\(b\)个\(a\)，这是一个幂塔函数，显然是不能够直接计算的。

  考虑欧拉降幂，如下：

\[a^b\equiv \begin{cases} a^{b\space \text{mod}\space \phi(m)+\phi(m)} &b\geq \phi(m)\\ a^b& b<\phi(m) \end{cases}(\text{mod}\space m)\]

  显然直接套用公式即可， \[a^{a^{a^{\dots}}} = a(a^{a^{a^{\dots}}}\text{mod}\space \phi(m)+\phi(m))(\text{mod}\space m)\]

  从上式可知，我们递归进行即可。

  如果\(a\)是无限的，即乘方塔的层数无限，那么显然欧拉降幂公式里的\(b\)(\(b\)在这里是\(a^{a^{a^{\dots}}}\))一定是恒大于\(\phi(m)\)，如果\(a\)的层数是有限的，那么我们在计算过程中就需要对\(b\)(\(b\)在这里是\(a^{a^{a^{\dots}}}\))与\(\phi(m)\)的大小进行判断。

  并且这里我们不知道最终的\(\phi(m)\)是多少，所以需要进行递归计算。具体细节见代码。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <algorithm>  
#include <iostream>  
#include <cstring>  
#include <string>  
#include <cstdio>  
#include <vector>  
#include <queue>  
#include <stack>  
#include <cmath>  
#include <set>  
#include <map>  
  
#define INF 0x7f7f7f7f  
#define MAXN 16005  
#define N 200005  
#define P 2  
//#define MOD 99991  
#define MOD(a, b) a >= b?a % b + b :a  
  
typedef long long ll;  
  
namespace fastIO {  
    //#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1<<22, stdin), p1 == p2) ? EOF : *p1++)  
 //char buf[(1 << 22)], *p1 = buf, *p2 = buf;  inline int read() {  
        char c = getchar(); int x = 0, f = 1;  
        while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }  
        while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();  
        return x * f;  
    }  
}  
  
using namespace fastIO;  
using namespace std; 
  
ll phi(ll x) {  
    ll res = x, a = x;  
    for (ll i = 2; i * i <= x; i++) {  
        if (a % i == 0) {  
            res = res / i * (i - 1);  
            while (a % i == 0) a /= i;  
        }  
    }  
    if (a > 1) res = res / a * (a - 1);  
    return res;  
}  
  
  
ll k_pow(ll a, ll b, ll p) {  
    ll res = 1;  
    while (b) {  
        if (b & 1) res = MOD(res * a, p);  
        a = MOD(a * a, p);  
        b >>= 1;  
    }  
    return res;  
}  
  
ll f(ll a, ll l, ll r, ll m) {  
    if (l == r || m == 1)return MOD(a, m);  
    ll k = phi(m);  
    return k_pow(a, f(a, l + 1, r, k), m);  
}  
  
  
  
  
int main() {  
    int T;  
    scanf("%d", &T);  
    while (T--) {  
        int a, b, m;  
        a = read(), b = read(), m = read();  
        if (b == 0)  
            printf("%d\n",1 % m);  
        else if (b == 1){  
            printf("%d\n", a % m);  
        }  
        else {  
            printf("%lld\n", f(a, 1, b, m) % (1ll * m) );  
        }  
    }  
    return 0;  
}